Typesetting text in math mode (2)

Posted on by

In a previous post (Typesetting text in math mode) I advertised the use of \mbox to write text in mathematical formulas. This works when you are in the "standard size", but looks funny if you have subscripts because the sizes are off:

$ 50 \mbox{ apples}_{\mbox{yellow}} \times 
100 \mbox{ apples}_{\mbox{red-green}} 
= \mbox{lots of apples}^{\mbox{to eat}} $

looks like
50 \mbox{ apples}_{\mbox{yellow}} \times 100 \mbox{ apples}_{\mbox{red-green}} = \mbox{lots of apples}^{\mbox{to eat}}

In these cases (and also in the standard cases but there it looks the same), you can use the command \text which will come out in the right font size. In addition to just \text, there is also \textbf (bold face), \textit (italics) and \texttt (typewriter).

$ 50 \text{ apples}_{\text{yellow}} \times 
100 \textit{ apples}_{\texttt{red-green}} 
= \textbf{lots of apples}^\text{to eat} $

looks like
50 \text{ apples}_{\text{yellow}} \times 100 \textit{ apples}_{\texttt{red-green}} = \textbf{lots of apples}^\text{to eat}

Note: Most of the time \text should just work in math mode without any packages, but for some distributions you need to explicitly load the package amstext or amsmath.

List your publications before the bibliography

Posted on by

Usually, in academic texts you cite stuff and at the end there is the bibliography that contains the full entries for all things referenced in the text. But there are some situations where you want to list some complete bibliography entries beforehand, somewhere in the text. For example you may want a list of prior work somewhere near the beginning of a grant proposal or a list of things published during the grant period somewhere at the end, but separate from the bibliography. Of course, you can write this list by hand, but where would be the fun in that?

And of course there is a LaTeX package for that, bibentry. You include the package with your bibliography style in the preamble. You can include it together with natbib.

\bibliographystyle{apalike} % or any other style you like
\usepackage{natbib} % optional, but combination is possible
\usepackage{bibentry}

Then, also in the preamble, you "turn off" the regular bibliography with \nobibliography. After that you can create your list of stuff somewhere in the document, but you will not have a bibliography at the end. Which is probably not what you want. So to additionally be able to include the references in the usual way, use this snippet:

\nobibliography*
\let\oldthebibliography=\thebibliography
\let\endoldthebibliography=\endthebibliography
\renewenvironment{thebibliography}[1]{%
   \begin{oldthebibliography}{#1}%
   \setlength{\parskip}{0ex}%
   \setlength{\itemsep}{0ex}%
}%
{%
   \end{oldthebibliography}%
}

The citing commands (\cite, \citep, etc.) and what they produce are unchanged, but now you can use \bibentry at any point in the text to create the full bibliographic entry. The formatting will be the same as for the references in the bibliography:

Parts of this work have been published in: \bibentry{Kessler2014}

Overlays and verbatim

Posted on by

Another weird LaTeX problem. I have a piece of code on my slide and the result it gives. I want to change the code slightly and visualize the change in the result. Normally in LaTeX beamer slides, I would use overlays like this:

Query:
\begin{verbatim}
some code
\alt<2>{slightly changed code on slide 2}{original code on slide 1}
some more code
\end{verbatim}

Result:
this item is the same in both
\visible<1>{this one is only there for the original code}
\visible<2>{this one is only there for the changed code}

So far, so good. The code is in a verbatim environment, so I have cannot put the overlay around the line I want to change, but that’s fine, let’s make it an alternative around the whole verbatim part. But, unfortunately, the problem is that you cannot put a verbatim environment inside of overlays (learn why). So you have to hack it. This is the code I want, the line with FILTER is the one I only want to have on the second slide:

\begin{verbatim}
SELECT ?book ?author ?releasedate
WHERE {
   ?book dbo:author ?author .
   {
      ?book dbp:releaseDate ?releasedate . 
   } UNION {
      ?book dbp:pubDate ?releasedate . 
   }
   FILTER (?releasedate > 1950)
}
\end{verbatim}

Like in my post on using verbatim inside of verbatim, I have to end the verbatim environment prematurely, skip back over the space and then I can include the overlay inside of verb.

\begin{verbatim}
SELECT ?book ?author ?releasedate
WHERE {
   ?book dbo:author ?author .
   {
      ?book dbp:releaseDate ?releasedate . 
   } UNION {
      ?book dbp:pubDate ?releasedate . 
   }
\end{verbatim}
\vspace{-0.5\baselineskip}
\verb|  |\visible<2>{\texttt{FILTER (?releasedate > 1950 )}}\\
\verb|}|
\\

Not the most elegant way, but it works…

Euclidean and cosine distance for unit vectors (and negative entries!)

Posted on by

Just a few quick words about the assumption we made in the last post about all our entries in the vectors being positive so that we can define the cosine distance as 1 minus the similarity. This assumption is actually not necessary. We can have negative entries, as long as our vectors are normalized to unit length everything still works.

Remember Euclidean distance for unit vectors:
d_{\text{euclid}}(\vec{p},\vec{q}) = \sqrt{2(1 - \sum_i p_i q_i)}

And cosine similarity for two unit vectors:
s_{\text{cosine}}(\vec{p},\vec{q}) = \sum_i p_i q_i

So now, like we did in the last post, let’s say we have two vectors v and w and we know that measured with Euclidean distance, v is closer to some other point p than w*:
d_{\text{euclid}}(\vec{p},\vec{v}) \leq d_{\text{euclid}}(\vec{p},\vec{w})

We do the same steps as in the last post, but then go on and get rid of the 1 and the minus (attention, this changes the direction of the inequality):
1 - \sum_i p_i v_i \leq 1 - \sum_i p_i w_i
\Leftrightarrow - \sum_i p_i v_i \leq - \sum_i p_i w_i
\Leftrightarrow \sum_i p_i v_i \geq \sum_i p_i w_i

Voila, cosine similarity!

So if p is closer to v than to w as measured with Euclidean distance, the cosine similarity of p and v is higher than that of p and w:
d_{\text{euclid}}(\vec{p},\vec{v}) \leq d_{\text{euclid}}(\vec{p},\vec{w}) \Leftrightarrow s_{\text{cosine}}(\vec{p},\vec{v}) \geq s_{\text{cosine}}(\vec{p},\vec{w})

So whenever you have unit length vectors and are only interested in relative distances, it shouldn’t make a distance whether you use Euclidean distance or cosine similarity.

* Same footnote as last time: The text says “closer” and not “closer or the same” and that is actually what I wanted to say, but there seems to be some strange bug in this LaTeX plugin that doesn’t allow you to use the < sign in a formula... so we'll take the less-or-equal sign and just ignore the equal-part.

Euclidean and cosine distance for unit vectors

Posted on by

The Euclidean distance between two vectors p and q is the length of the line segment that connects them (here and in all following formulas the sum is over all dimensions of the vectors, i.e., if we have n dimensions the sum ranges from i=0 to n):
d_{\text{euclid}}(\vec{p},\vec{q}) = |\vec{p} - \vec{q}| = \sqrt{\sum_i (p_i - q_i)^2}

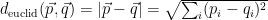
Using the binomial expansion, we can write this as follows:
d_{\text{euclid}}(\vec{p},\vec{q}) = \sqrt{\sum_i p_i^2 - 2\sum_i p_i q_i +\sum_i q_i^2}

Unit vectors have a length of 1 (by definition), length is calculated as the Euclidean norm, that is, the Euclidean distance of a vector to the zero vector, i.e., the square root of the sum of all sqared entries in the vector:
|\vec{p}| = d_{\text{euclid}}(\vec{p},0) = \sqrt{\sum_i (p_i-0)^2 } = \sqrt{\sum_i p_i^2 }

If something is 1, its square is also 1:
\sqrt{\sum_i p_i^2 } = 1 \Leftrightarrow \sum_i p_i^2 = 1

We can now replace the squared sums over all vector elements in the formula for Euclidean distance with 1:
d_{\text{euclid}}(\vec{p},\vec{q}) = \sqrt{1 - 2\sum_i p_i q_i + 1} = \sqrt{2 - 2\sum_i p_i q_i} = \sqrt{2(1 - \sum_i p_i q_i)}

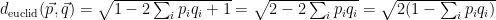
Now let’s see how the cosine distance is defined. The more common thing to do is to calculate the cosine similarity of two vectors as the cosine of the angle between them:
s_{\text{cosine}}(\vec{p},\vec{q}) = \frac{\vec{p} \cdot \vec{q}}{|\vec{p}| |\vec{q}|} = \frac{\sum_i p_i q_i}{|\vec{p}| |\vec{q}|}

As we have unit vectors, we can get rid of the division by the length (which is always 1), so the formula is simplified to the dot product between the two vectors:
s_{\text{cosine}}(\vec{p},\vec{q}) = \sum_i p_i q_i

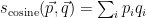
When we have a vector space where the entries correspond to occurrences of terms in a document, all entries are positive, so the value of the cosine similarity will always be between zero and one. This means, we can define the cosine distance as:
d_{\text{cosine}}(\vec{p},\vec{q}) = 1 - s_{\text{cosine}}(\vec{p},\vec{q}) = 1 - \sum_i p_i q_i

So let’s put it together. Let’s say we have two vectors v and w and we know that measured with Euclidean distance, v is closer to some other point p than w is*:
d_{\text{euclid}}(\vec{p},\vec{v}) \leq d_{\text{euclid}}(\vec{p},\vec{w})

We can now replace the Euclidean distance with the formula from above, square both sides (because that doesn’t change the inequality relation) and get rid of the two that appears on both sides:
\sqrt{2(1 - \sum_i p_i v_i)} \leq \sqrt{2(1 - \sum_i p_i w_i)}
\Leftrightarrow 2(1 - \sum_i p_i v_i) \leq 2(1 - \sum_i p_i w_i)
\Leftrightarrow 1 - \sum_i p_i v_i \leq 1 - \sum_i p_i w_i

What we are left with is the cosine distance! So, putting start and end together, what we have shown is:
d_{\text{euclid}}(\vec{p},\vec{v}) \leq d_{\text{euclid}}(\vec{p},\vec{w}) \Leftrightarrow d_{\text{cosine}}(\vec{p},\vec{v}) \leq d_{\text{cosine}}(\vec{p},\vec{w})

This doesn’t mean that when you calculate Euclidean distance and cosine distance between two vectors that you will get the same number. But whenever you are only interested in relative distances (that means you only want to know which of two vectors is closer to something than the other) and you have vectors that are normalized to unit length with only positive entries, then the result should be the same whether you use cosine or Euclidean distance.

* The text says “closer” and not “closer or the same” and that is actually what I wanted to say, but there seems to be some strange bug in this LaTeX plugin that doesn’t allow you to use the < sign in a formula... so we'll take the less-or-equal sign and just ignore the equal-part.

Midi playback with Timidity

Posted on by

Timidity is a little commandline program to play midi files on Linux:

timidity Was-soll-das-bedeuten.midi

My midi is a choir score with three voices and the output of timidity looks like this:

Playing Was-soll-das-bedeuten.midi
MIDI file: Was-soll-das-bedeuten.midi
Format: 1  Tracks: 6  Divisions: 384
Sequence: control track
Text: creator: 
Text: GNU LilyPond 2.18.2           
Track name: :Soprano
Track name: :Alto
Track name: :Men

With the above standard command all voices are played together. To practice something it is sometimes nice to have only your own voice alone, you can do this by quieting/muting all voices except your own. The voices to be muted are listed after the option -Q separated by comma. The value 0 means all voices, the number of the other voices is given by their order in the output. So in the file I have, Soprano would be 1, Alto 2 and the men’s voices 3. Including the number mutes the voice, including it with a minus sign plays it. So let’s say I want to practice the alto voice, I’ll mute all but voice 2:

timidity -Q 0,-2 Was-soll-das-bedeuten.midi

It’s also simple to transpose stuff, this will play the song two semitones higher:

timidity -K 2 Was-soll-das-bedeuten.midi

Using GIMP to draw a rectangle

Posted on by

GIMP is not your typical program for drawing, but is is the only thing related to graphics that is installed on my linux. So I have this screenshot and I want to draw a red rectangle around the part that needs to be clicked. This is how:

  1. Open your graphic file with GIMP.
  2. Use the "Rectangle Select Tool" and mark the place where you want your rectangle to be.
  3. Select the color you want to draw the rectangle in as foreground color (in my case that would be red).
  4. In the menu "Edit" choose "Stroke selection".
  5. In the dialogue that comes up, choose "Stroke line" with "solid colour" (it will take the current foreground color), you can adjust the width and if you open up "Line style" you can do more things (e.g., rounded edges).
  6. Click "Stroke" and voila!

Executing a command on a remote server

Posted on by

This is probably a very old hat for Linux-savy people. You can use ssh to execute commands on a remote server, just pass them on as an additional argument:

ssh me@my.server.de "cd bla ; ls ; python test.py "

I use double quotes (“) istead of single quotes (‘) to interpret variables. Different commands are separated with semicolon (;). You can use any command you like, but for some reason when I call some GUI I don’t get the output on the command line until the window is closed.

Open SSH folder in Dolphin using a SSH-key

Posted on by

Dolphin allows you to connect to folders on other machines per SSH, but there is no option to specify a key file. But you can add the key to your general SSH configuration (with the added benefit that you also won’t have to specify the keyfile anywhere else, no more -i on the command line!). This is how it works:

  1. Locate your private key file, say it’s ~/.ssh/myidentity_rsa.
  2. Open or create the file ~/.ssh/config and add the lines 
    Host myhost.net
  HostName myhost.net
  IdentityFile ~/.ssh/myidentity_rsa
  3. Type fish://user@myhost.net/path/to/folder/ into the location bar.
  4. Now it should ask for the passphrase to your key.

Done!